Fourier–Motzkin elimination
Fourier–Motzkin elimination, FME method, is a mathematical algorithm for eliminating variables from a system of linear inequalities. It can look for both real and integer solutions. Its computational complexity is double-exponential.
Elimination (or ∃-elimination) of variables V from a system of relations (here, linear inequalities) consists in creating another system of the same kind, but without the variables V, such that both systems have the same solutions over the remaining variables.
If one eliminates all variables from a system of linear inequalities, then one obtains a system of constant inequalities, which can be trivially decided to be true or false, such that this system has solutions (is true) if and only if the original system has solutions. As a consequence, elimination of all variables can be used to detect whether a system of inequalities has solutions or not.
Let us consider a system  of
of  inequalities with
inequalities with  variables
variables 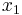 to
to 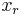 , with
, with 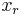 the variable to eliminate. The linear inequalities in the system can be grouped into three classes, depending on the sign (positive, negative or null) of the coefficient for
the variable to eliminate. The linear inequalities in the system can be grouped into three classes, depending on the sign (positive, negative or null) of the coefficient for 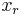 :
:
- those that are equivalent to some inequalities of the form
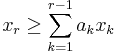 ; let us note these as
; let us note these as 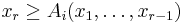 , for
, for  ranging from 1 to
ranging from 1 to 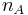 where
where 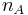 is the number of such inequalities;
is the number of such inequalities; - those that are equivalent to some inequalities of the form
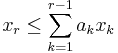 ; let us note these as
; let us note these as 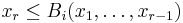 , for
, for  ranging from 1 to
ranging from 1 to 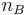 where
where 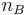 is the number of such inequalities;
is the number of such inequalities; - those in which
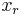 plays no role, grouped into a single conjunction
plays no role, grouped into a single conjunction  .
.
The original system is thus equivalent to 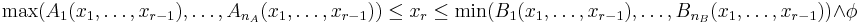 .
.
Elimination consists in producing a system equivalent to 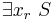 . Obviously, this formula is equivalent to
. Obviously, this formula is equivalent to 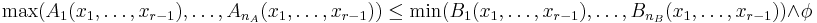 .
.
The inequality 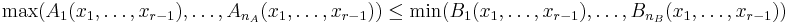 is equivalent to
is equivalent to 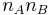 inequalities
inequalities 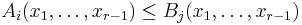 , for
, for 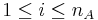 and
and 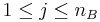 .
.
We have therefore transformed the original system into another system where 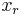 is eliminated. Note that the output system has
is eliminated. Note that the output system has 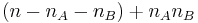 inequalities. In particular, if
inequalities. In particular, if 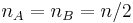 , then the number of output inequalities is
, then the number of output inequalities is 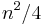 .
.
The operation is named after Joseph Fourier and Theodore Motzkin.
See also
- Real closed field: the cylindrical algebraic decomposition algorithm performs quantifier elimination over polynomial inequalities, not just linear
References
- Schrijver, Alexander (1998). Theory of Linear and Integer Programming. John Wiley & sons. pp. 155–156. ISBN 0471982326.
- Keßler, Christoph W.. "Parallel Fourier–Motzkin Elimination". Universität Trier. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.54.657&rep=rep1&type=pdf.
- Williams, H. P. (1986). "Fourier's Method of Linear Programming and its Dual". American Mathematical Monthly 93: 681–695.
External links
- Lectures on Convex Sets, notes by Niels Lauritzen, at Aarhus University, March 2010.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||